The majority of PLGA type polymers are linear in nature, with the exception of those generated using polyfunctional initiators, such as glucose, or those for which specific chemical modifications have been applied to achieve specific architectures. Through the use of gel-permeation-chromatography quaternary detection (GPC-4D), Akina, Inc. has developed techniques around measuring the branching status of PLGAs by leveraging the reduction in viscosity caused by reduced hydrodynamic radius present for a branched PLGA as compared to its linear counterpart1,2. Doing this requires carefully establishing critical parameters including the dn/dc as well as the drainage factor, both of which are affected by the lactide:glycolide (LA:GA) ratio of PLGA3,4.
As a quick, rule-of-thumb, if the intrinsic viscosity of a sample measured by the same methodology matches or exceeds that of a linear comparator at a given molecular weight which is representative of the average molecular weight of the sample, then it is highly probable that the sample is linear in structure. Utilizing data obtained from PLGA linear standards generated at Akina, Inc, composite Mark-Houwink profiles were generated for PLGA 50:50, 75:25, and 100:0 (PDLLa).
Table 1. Data used in Mark-Houwink calculations as obtained by GPC-4D analysis at Akina, Inc.
| Polymer Standard | Molecular Weight (Mn, Mw, Mz) |
Intrinsic Viscosity at (Mn, Mw, Mz) |
|---|---|---|
| PLGA 50L-S Lot #180329RAI-A | 5834 | 10.985 |
| 8303 | 13.48 | |
| 10890 | 15.74 | |
| PLGA 50L-M Lot #180406RAI-A | 16280 | 20.63 |
| 23790 | 25.02 | |
| 29700 | 27.803 | |
| PLGA 50L-H Lot #190314RAI-A | 42620 | 37.926 |
| 52530 | 42.13 | |
| 64490 | 46.949 | |
| PLGA 50L-H-E Lot #240202RAI-A) | 34880 | 32.49 |
| 45730 | 37.25 | |
| 58560 | 42.47 | |
| PLGA 50L-H-E Lot #201210RAI-A | 49038 | 40.012 |
| 59050 | 43.799 | |
| 72630 | 48.617 | |
| PLGA 75L-M Lot #180323RAI-A | 16290 | 21.624 |
| 25370 | 27.97 | |
| 33700 | 32.668 | |
| PLGA 75L-S Lot #180410RAI-A | 12180 | 17.52 |
| 17830 | 22.04 | |
| 22420 | 25.121 | |
| PLGA 75L-H Lot #180313RAI-B | 76170 | 57.63 |
| 96330 | 65.14 | |
| 110500 | 69.288 | |
| PLA 100L-S Lot #180312FAJ-A | 8142 | 12.888 |
| 15890 | 18.75 | |
| 39590 | 36.635 | |
| PLA 100L-M Lot #180306FAJ-A | 24900 | 27.819 |
| 33900 | 33.69 | |
| 40400 | 37.381 | |
| PLA 100L-H Lot #180302RAI-A | 103200 | 69.074 |
| 132700 | 78.942 | |
| 190200 | 96.207 |
This data was plotted to form composite plots for indicated PLGAs (La:Ga ratio).
Figure 1. Mark-Houwink plots of PLGA 50L, 75L, and 100L, respectively.
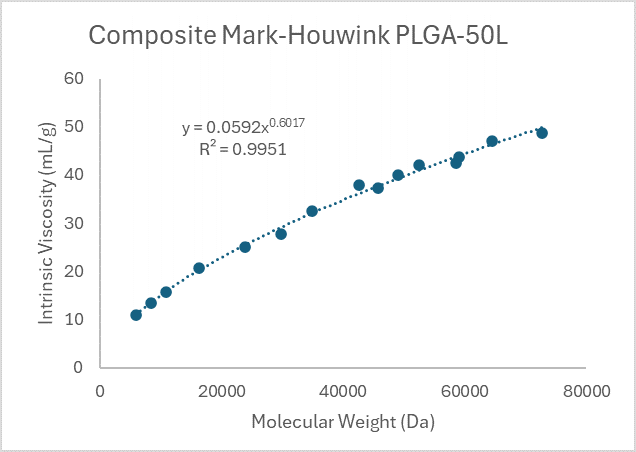
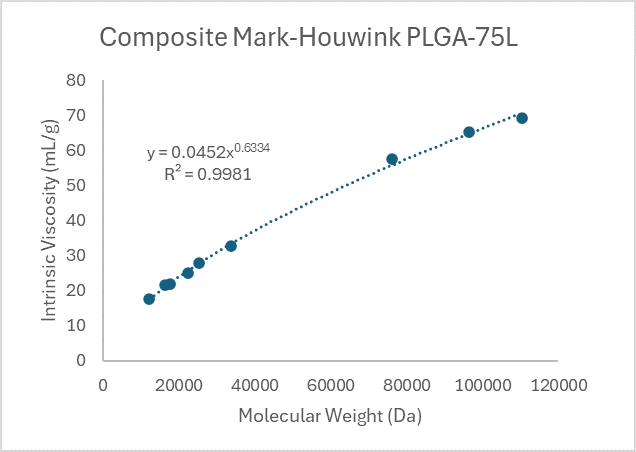
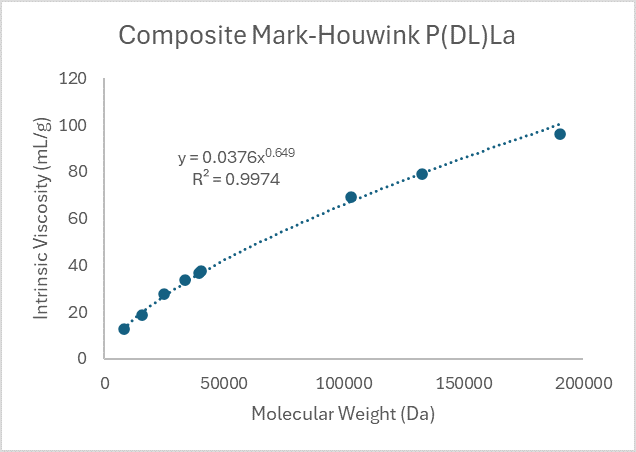
From this the following Mark-Houwink Parameters were derived for linear polymers. Note that the Mark-Houwink profile of each GPC run naturally varies due to normal experimental error and these just provide a general average of the profile across a series of representative linear runs. Additionally, the standard error of the data from the regression was calculated based on the R2 value. For this, the following equations were applied.
Mark-Houwink equation: Intrinsic viscosity = K*(Molecular Weight)a
Standard Error: SE = ((1-R2)/N-2)(1/2)
| PLGA (La:Ga) | Slope constant (K) | Exponent (a) | Standard error |
|---|---|---|---|
| 50:50 | 0.0592 | 0.6017 | 0.0194 |
| 75:25 | 0.0452 | 0.6334 | 0.926 |
| 100:0 | 0.0376 | 0.649 | 0.926 |
Based on this data, an estimation as to whether a sample is primarily comprised of linear PLGA or possibly branched based on the number average molecular weight (Mn) and the intrinsic viscosity at number average molecular weight ([η]n (mL/g)) can be found using the calculator above to determine if the samples viscosity is reduced relative to known linear standards within normal experimental error (2 x standard error lower, 95% bounded range).
Like all measurements, these parameters are susceptible to experimental error. Additionally, this only applies to data obtained under the conditions present in GPC-4D (acetone, 25 C, flow conditions, Mn fraction specifically) and should not be extrapolated to inherent viscosity obtained using other methods. If you would like to discuss branch measurements of your samples, please contact us.